How Warm Were the 1930's?
Presented largely without comment, for those who got caught up in the summer-of-the-shark-style "hottest summer ever" coverage this year. US only:
I think most would agree that the heat waves of 1936 had about zero to do with man-made CO2 (since it preceded significant increases in Co2 since 1950). It was just freaking hot. When it happened in 1936, people treated it as a natural disaster. Today, we would likely treat it as an excuse to shut down the world economy.
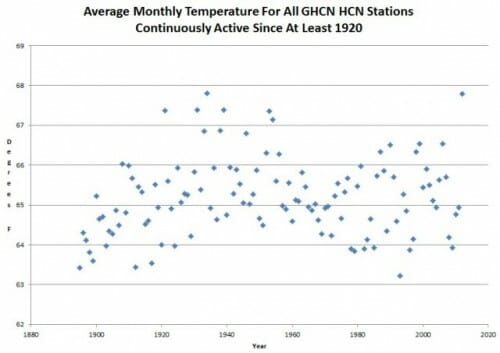
PS - Most warming data you see is biased by the fact that it relies on a lot of thermometers that exist today but did not exist in the 1930's. If you limit the official government data set to only thermometers that have existed since at least 1920 you get this picture of us "warming". This last year was historically quite hot, but not unprecedentedly so (again, US data only)

I am a GW skeptic, and the thing that makes me angriest about the pro-warming crowd is when they cherry pick data.
However, these two charts, especially the first one, seem to be cherry-picked data as well. 110 degrees fahrenheit would seem to be a pretty high bar - meaning that it would occur very infrequently and in very few places in the US. I could envision a 1 to 2 degree change in underlying average temperature not having much of an effect on how often these dramatic spikes occur. So, this first chart might be irrelevant regarding whether or not there has been global warming.
The second chart might suffer from the opposite problem, where the data is over smoothed by taking the daily temperatures in a given month and averaging them, and then averaging those averages into an annual average. It would seem that the GW people could argue that this smoothing would mask hotter summers by averaging them down with cooler winters.
Let me be clear - I am not asserting that I am right about this, and I am not arguing for global warming. It is simply that as a semi-engaged skeptic, I get so sick of each side cherry picking data sets that support their arguments.
I'd like to see more info about the source. Clicking through to about the third website reveals only the same chart #1, but not the source.
Having said that, I wonder what would you would suggest instead of, or along with the first chart? Observations by temperature bands?
Even so, because 110 degrees Fahrenheit is an extreme temperature (relative to our experience of recent decades), the sheer numbers do appear make a reasonable point counter to expectations of a warming world. That said, without knowing some basics about the facts presented (e.g. are the observations in chart #1 from the "same locations" over that expanse of time?) one would have to reserve some judgement.
As for graph #2, perhaps the median vs average, and perhaps three monthy medians: daily high, daily low, daily average...not unlike the "candle stick" charts for stocks? I wonder if that level of detail would add more information when it comes to GW...may be interesting if we see the top to bottom delta increasing over time. Might also be interesting to see the "best fit" regression line for the data points on #2. Eyeballing it, if you take out the outliers, it looks rather flat.
The period around 1938-1939 saw warmer temperatures in the Arctic than at present. That was the peak in the last natural 60 year cycle, which then peaked again in 1998. There is a longer ~1000 year cycle which should pass a maximum within 50 to 200 years from now. It's all natural and has nothing to do with any radiative greenhouse effect, as explained below.
Some time back I asked people if they could explain how the required thermal energy gets into the surface of Venus. At least 98% of all incident Solar radiation is absorbed by the thick atmosphere there, so the Sun does not heat the surface significantly with direct radiation.
No one on any climate blog has provided the correct answer, so I guess it's time to explain what does happen.
The thermal gradient in an atmosphere evolves even in still air. We have proof that it does in over 800 experiments by Roderich Graeff, and it is logical that it would if you consider my thought experiment about a cylinder divided into three sections. If the top and bottom sections are a vacuum and then gas is released from the middle section by removing the dividers, then, at thermodynamic equilibrium, there has to be a cooler temperature at the top and warmer at the bottom. If KE were homogeneous, then the extra PE in the molecules at the top would cause a general propensity for some gas to move downwards gaining KE as it does so. After all, each individual molecule has mass, and thus has KE (as we know) and also PE. So it must obey Newton’s laws in free flight between impacts.
The Venus surface would not be as hot if all convection moved away from the surface. If that happened we have no explanation as to how the required energy gets into the Venus surface. Because IPCC and cohorts could not conceive this heat transfer by convection, they postulated that back radiation could do the job of raising Earth’s surface 33 degrees, and the surface of Venus by about 500 degrees. But 10W/m^2 of direct solar radiation reaching the Venus surface could hardly produce much back radiation anyway! Surface bound heat transfer by convection is the missing link which we have all been looking for, and no one it seems has previously described this as being the only explanation.
We must understand that diffusion of KE (even in still air) sets the gradient of the thermal plane in an atmosphere. Then any additional heat absorbed from the Sun (such as when night becomes day) will spread out over that thermal plane (moving away from the source in all 3D directions) just as if it were the level surface of a lake receiving rain (extra water) in some section of the lake. This is the only way we can explain how energy moves up the thermal gradient and into the surface of Venus. Radiation cannot transfer heat from the cooler atmosphere, but non-radiative convection can flow towards the surface over the thermal plane whose gradient is set by diffusion of KE in a gravitational field.